高校から理系の道を進んできた。高校時代は素数とか整数とか好きで(多分自分は変わっているんだと思う)、数学にも面白さを感じていた。
「素数が無限にあることを証明する」とか、「各桁の数字の和が3の倍数になるなら、その数は3で割り切れることを証明する」とか、そういった問題を解くのも楽しかった。
「数」に興味がある人が世の中にどのくらいいるのかわからないけど、多くの人々を魅了しているであろう数字がある。それは、
1.6180339887……
ご存知の人がどれくらいいるだろうか、これは黄金数と呼ばれ、1:1.6180…は黄金比と呼ばれる。
フィボナッチ数列とも関係が深い*この数字は数学好きのためだけのものではない。あらゆる場面で出てくるのだ。
*フィボナッチ数列は前の2つの数字の和を並べた数列 (1, 1, 2, 3, 5, 8, 13, 21, 34…..)。フィボナッチ数列の隣り合う2項の比は黄金比に近づいていく(例えば、8/5=1.6、34/21=1.619..)
以下の本は黄金比について豊富な情報と知識で語り続けていて、黄金比好きにはたまらない書籍となっている。
「黄金比はすべてを美しくするか?―最も謎めいた「比率」をめぐる数学物語 (ハヤカワ文庫NF―数理を愉しむシリーズ)」著者マリオ・リヴィオ

久々に手にとって読み返してみたら、改めて勉強になったので、今回記事にまとめるものです。
黄金比とは
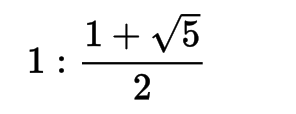
の比であり、1:1.6180…となる。この数字は世界のいろいろなところに現れる。
過去の数学者や美術家にも愛され、絵画の中にも出てくることは有名。明確な証拠がないものもあるとのことだが、モナリザやパルテノン神殿など、黄金比で語られる作品が多数ある。
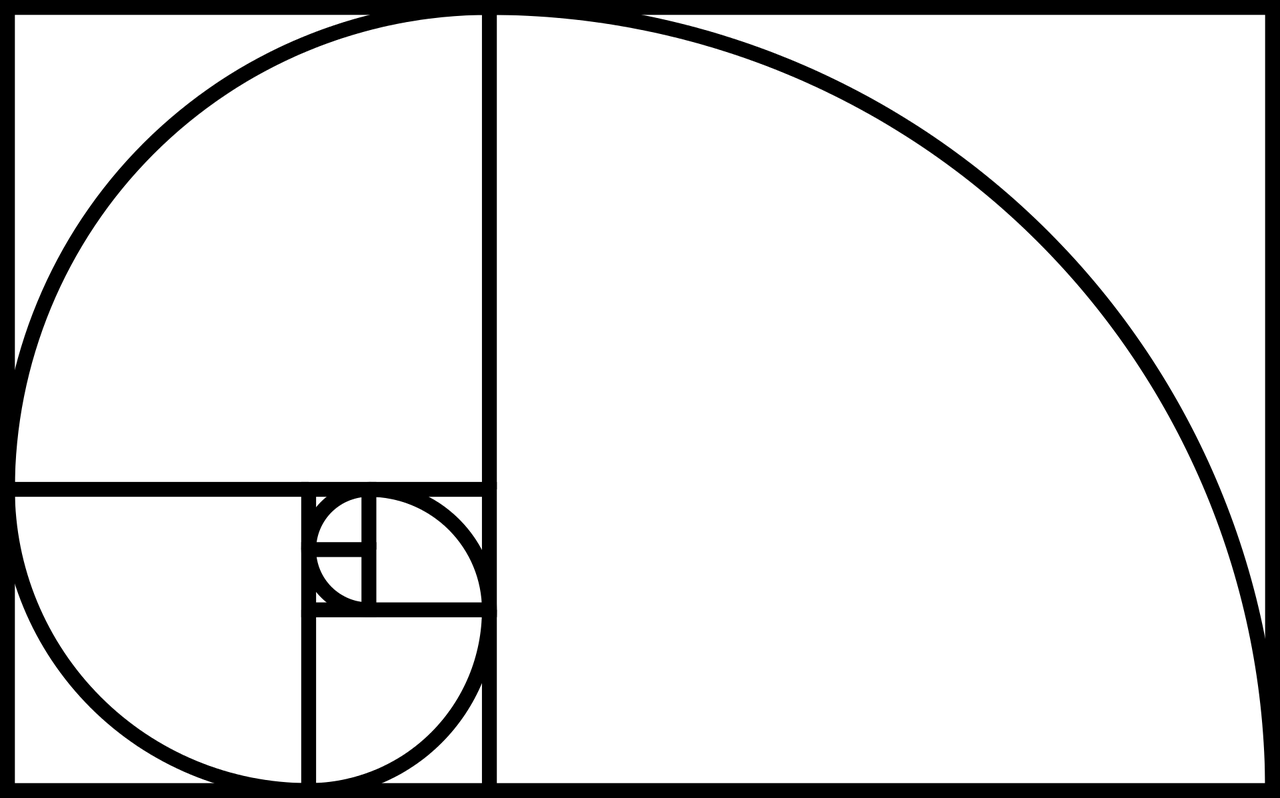
黄金比と対数らせんも表裏一体の関係にあるが、対数らせんは自然界でも多数見受けられる。ハヤブサの飛行コースや、天の川のように同じ平面に集まった星々にも対数らせんが見つかるし、花びらや葉の配置にも現れるとのこと。

それだけではなく、株価の動きにまで黄金比が出てくる。ウソだと思うなら「黄金比 株価」でGoogleで調べてみてほしい。
また、黄金比は「美しくする数字」としても知られ、「美人顔と黄金比」なんかでまとめられているウェブサイトも見つかる。
「黄金比メイク設計図から作る、美人メイク術。」なんてタイトルまであるようだ。
黄金比なんて関係ないわ、と思っている女性の皆さんも無視できない数字なのである。
ブログと黄金比
ブロガーのみなさんで、サイト設計に数学を使用している人がどこまでいるか分からない。実はこだわりを持っている人もいるのかなと思う。
黄金比を適用したサイトデザインを行っているデザイナーもやはりいるみたい。
僕のサイトのサムネイル画像(トップページの各投稿のサムネイル画像)や各記事の一番上に表示されるアイキャッチ画像の縦横比は黄金比になるように設定している。
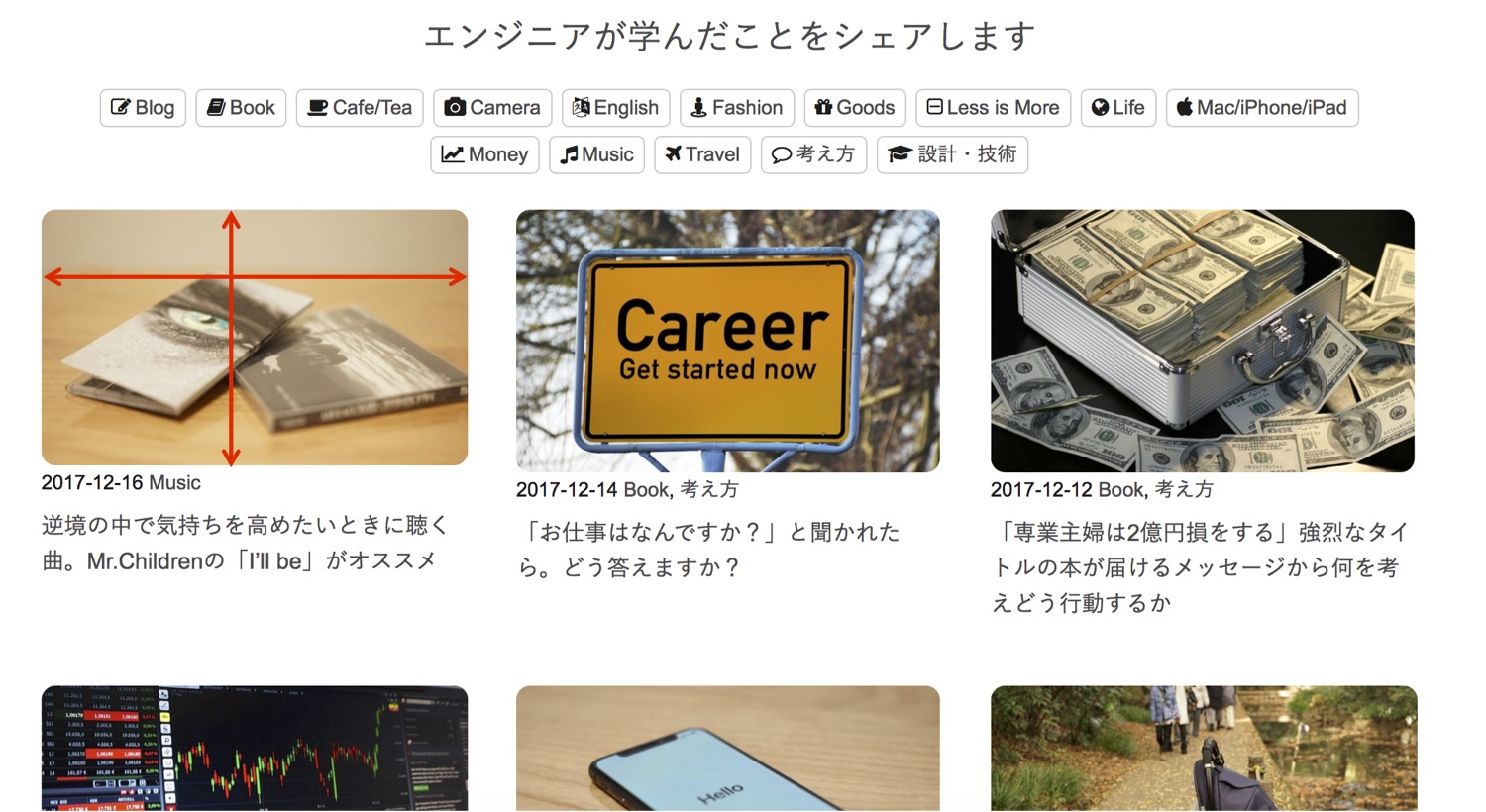

実はオリジナルテーマを作っているときにはすっかり黄金比の存在を忘れていたのだが、あるとき思い出して、サムネイル画像の縦横比を調整した。
気づく人なんていないと思う。
でも自分のブログの設計者として、こだわり持ってサイトを作るというのは楽しいもの。細部へのこだわりをつき詰めていきながら、よりよいサイトを作成していきたい。
では。
「黄金比はすべてを美しくするか?―最も謎めいた「比率」をめぐる数学物語 (ハヤカワ文庫NF―数理を愉しむシリーズ)」著者マリオ・リヴィオ@Amazon



















